새롭게 구축할 3D 공간에 대한 설명
Y-up Right Handed Coordinate(오른손 좌표계)

X axis의 용도 : 좌,우 구분(Pitch)
Y axis의 용도 : 위,아래 구분(Yaw)
Z axis의 용도 : 앞,뒤 구분(Roll)
3D Rotation에 대한 고찰
회전이란 공간 변환의 관점에서 어떤 행동인지 기술하시오
- 물체가 아닌 공간이 돌아가는 것.(월드 공간이 아닌 해당 물체가 속한 공간이 회전하는 것)
- 변환 후 각 벡터의 크기가 1이여야 함.
- 각 벡터가 서로 직교해야 함.
3D 회전을 위해 Yaw/Roll/Pitch를 값을 따로 저장하는 이유를 설명하시오.
- 메모리를 아끼기 위해(Matrix보다 Float가 모든 변환에 있어서 값이 더 저렴하기때문)
각 축에 대한 회전 행렬을 생성할 때 왜 Y축은 반대인지 이유를 설명하시오.
$R_{x} = \begin{bmatrix}
1 & 0 & 0 \\\
0 & cos\theta & -sin\theta \\\
0 & sin\theta & cos\theta
\end{bmatrix} \quad
R_{y} = \begin{bmatrix}
cos\theta & 0 & sin\theta \\\
0 & 1 & 0 \\\
-sin\theta & 0 & cos\theta
\end{bmatrix} \quad
R_{z} = \begin{bmatrix}
cos\theta & -sin\theta & 0 \\\
sin\theta & cos\theta & 0 \\\
0 & 0 & 1
\end{bmatrix}$
- 모든 축들이 같은 방향으로 회전해야 하는데 오른손 좌표계 같은 경우는 반시계 방향으로 회전을 합니다.
그러나, Y축의 값이 반대이지 않을 경우에는 아래와 같이 회전 할 시 -로 가기 때문에 y축 회전의 sin값의 부호만
다르게 변화를 준 것이라고 생각합니다.
$Ry = \begin{bmatrix} cos\theta & 0 & -sin\theta \\\ 0 & 1 & 0 \\\ sin\theta & 0 & cos\theta \end{bmatrix} \begin{bmatrix} 0 \\\ 1 \\\ 0 \end{bmatrix} = \begin{bmatrix} -sin\theta \\\ 0 \\\ cos\theta \end{bmatrix}= \begin{bmatrix} -1 \\\ 0 \\\ 0 \end{bmatrix}$
3D 회전 행렬
R(yaw) R(pitch) R(roll) 의 순서로 회전 행렬을 곱해서 최종 로컬 Forward, Right, Up의 값을 구하시오.
수기로 직접 계산해서 결과물을 증빙할 것.
$Yaw = (y)y, \quad Pitch = x(p), \quad Roll = z(r)$
$\begin{align}
R_{y} \cdot R_{p} \cdot R_{r} & = \begin{bmatrix}
cosy & 0 & siny \\\
0 & 1 & 0 \\\
-siny & 0 & cosy
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\\
0 & cosp & -sinp \\\
0 & sinp & cosp
\end{bmatrix}
\begin{bmatrix}
cosr & -sinr & 0 \\\
sinr & cosr & 0 \\\
0 & 0 & 1
\end{bmatrix} \\\
& = \begin{bmatrix}
cosy & siny \cdot sinp & sosy \cdot cosp \\\
0 & cosp & -sinp \\\
-siny & cosy \cdot sinp & cosy \cdot cosp
\end{bmatrix}
\begin{bmatrix}
cosr & -sinr & 0 \\\
sinr & cosr & 0 \\\
0 & 0 & 1
\end{bmatrix} \\\
& = \begin{bmatrix}
cosy \cdot cosr + siny \cdot sinp \cdot sinr & cosy \cdot (-sinr) + siny \cdot sinp \cdot cosr & siny \cdot cosp \\\
cosp \cdot sinr & cosp \cdot cosr & -sinp \\\
(-siny) \cdot cosr + cosy \cdot sinp \cdot sinr & siny \cdot sinr + cosy \cdot sinp \cdot cosr & cosy \cdot cosp
\end{bmatrix}
\end{align}$
카메라 뷰 좌표계
뷰 좌표계는 카메라 뒤쪽으로 향하는 방향이 +z인 좌표계이다.
목표 지점 정보가 주어진다면 이를 토대로 카메라의 회전 행렬을 제작하는 전체 과정을 유도 하시오.
- 타겟의 위치와 카메라의 위치를 알면 카메라 뷰 기준 표준기저벡터를 구할 수 있다.
- 각 벡터의 크기는 1입니다.
- Forward는 카메라위치 - 타겟위치 로 구할 수 있습니다.

- 그 다음 Right는 World의 Y축으로부터 Forward 방향으로 회전시켜줍니다.

- 그 후 마지막으로 Up은 Forward로부터 Right 방향으로 회전시켜줍니다.

이 때 예외적으로 주의해야 할 사항에 대해 추가하시오.
- ViewMatrix에서 $(TR)^-1 = R^{-1} T^{-1}$ 인 점을 유의해야 함.
이동과 회전이 고려된 카메라 행렬을 유도하시오.
- 직교행렬이기 때문에 회전 할 경우 전치하면 항등 행렬이 나옴.
- 회전행렬의 역행렬은 회전행렬을 전치한 것 입니다.
$\begin{align}(TR)^-1 & = R^{T}\cdot T^{-1} \\\
& = \begin{bmatrix}
cosr & -sinr & 0 \\\
sinr & cosr & 0 \\\
0 & 0 & 1
\end{bmatrix} \\\
& = \begin{bmatrix}
cosy \cdot cosr + siny \cdot sinp \cdot sinr & cosy \cdot (-sinr) + siny \cdot sinp \cdot cosr & siny \cdot cosp \\\
cosp \cdot sinr & cosp \cdot cosr & -sinp \\\
(-siny) \cdot cosr + cosy \cdot sinp \cdot sinr & siny \cdot sinr + cosy \cdot sinp \cdot cosr & cosy \cdot cosp
\end{bmatrix}^T
\begin{bmatrix}
1 & 0 & 0 & -x \\\
0 & 1 & 0 & -y \\\
0 & 0 & 1 & -z \\\
0 & 0 & 0 & 1
\end{bmatrix} \\\
& = \begin{bmatrix}
cosy \cdot cosr + siny \cdot sinp \cdot sinr & cosp \cdot sinr & (-siny) \cdot cosr + cosy \cdot sinp \cdot sinr & 0 \\\
cosy \cdot (-sinr) + siny \cdot sinp \cdot cosr & cosp \cdot cosr & siny \cdot sinr + cosy \cdot sinp \cdot cosr & 0 \\\
siny \cdot cosp & -sinp & cosy \cdot cosp & 0 \\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -x \\\
0 & 1 & 0 & -y \\\
0 & 0 & 1 & -z \\\
0 & 0 & 0 & 1
\end{bmatrix}
\end{align}$
카메라를 (0, 0, -500)에 두고 원점에 위치한 큐브를 와이어프레임으로 렌더링한 이미지 ( 1 단계 )

회전 행렬을 적용해 입력에 따라 Yaw, Roll, Pitch 회전을 진행한 움짤 이미지 ( 2단계 )
Yaw

Pitch

Roll

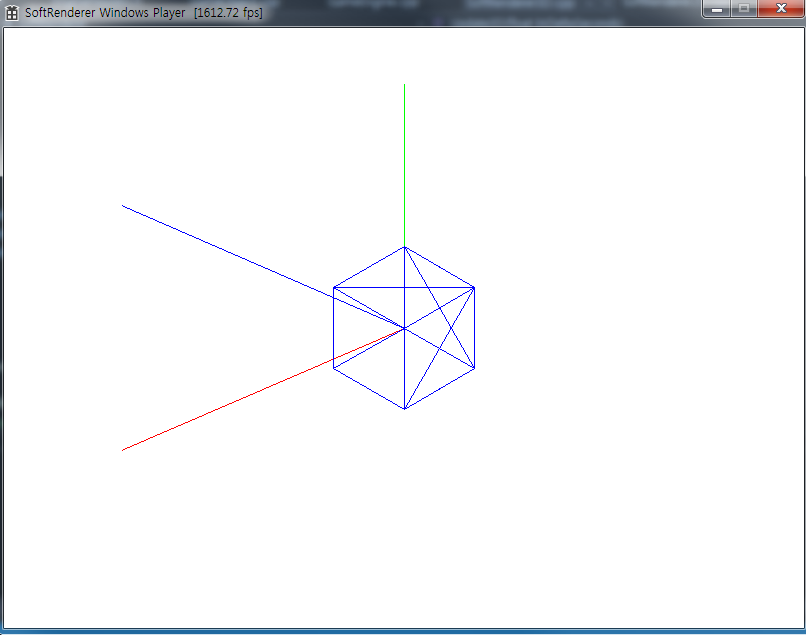
카메라를 (500, 500, -500)으로 이동하고 원점을 향해 보는 구도를 생성하시오. ( 3단계 )
'게임제작기법연구' 카테고리의 다른 글
| 게임제작기법연구 13주차 (0) | 2020.07.07 |
|---|---|
| 게임제작기법연구 12주차 (0) | 2020.06.29 |
| 게임제작기법연구 10주차 (0) | 2020.06.16 |
| 게임제작기법연구 8주차 (0) | 2020.06.02 |
| 게임제작기법연구 7주차 (0) | 2020.05.26 |