Affine Combination에 대해 설명하시오.
아핀조합이란 점+점 = 점 이 유일한 조건을 뜻한다.
각 점에 스칼라를 곱한 후 더해주는 것으로 각 점 X와 Y에 스칼라 a, b를 곱해주면
aX + bY = 점 으로 결과가 나오며 이 때 a+b = 1이 나오는 경우이다.
a+b = 1 이므로, b = 1-a로 바꿀 수 있으며 aX + (a-1)Y = 점이 된다.
단 모든 계수의 합이 1일 때 닫혀있다(점) 라고 한다.
BaryCentric Coorinate에 대해 설명하시오
무게중심이라고 부르며, 각 스칼라 값을 따로 모아서 좌표를 비교하는 것으로.
즉 (a, b)가 되며, 그것을 무게중심 좌표라고 부른다.
BaryCenter = 새롭게 두 점을 덧셈으로 조합해서 새롭게 생성 된 점
Barycentric Coordinate = 무게중심을 만드는데 기여한 스칼라 값들을 서로 묶어서 벡터로 만든 것
Line, Ray, Line Segment 각각의 생성 조건은?
위에 아핀 조합을 설명할 때 말한 aP1 + (a-1)P2 = P3 이 나오는 조건을 생각해 보자.
a = 0 이면 P3 = P2 이 되고
a = 1 이면 P3 = P1 이 된다.
a = 0.5 이면 P3 = 0.5P1+0.5P2 가 된다.
a = ∞ 이면 a쪽 방향으로 계속 직진하게 된다.
a = -∞ 이면 P2쪽으로 계속 증가하게 된다.
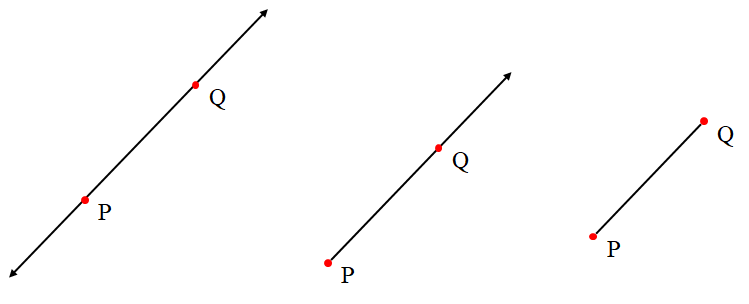
직선(Line) : -∞ < a < ∞
반직선(Ray) : 0 ≤ a < ∞
선분(Line Segment) : 0 ≤ a ≤ 1
Convex가 가지는 특징을 설명하시오.
아래 사진에서 회색으로 칠해진 부분은 무수한 점으로 이루어 진 공간이다.
이 안에 있는 어떤 두 점을 연결해도 연결 된 선분이 도형의 영역 안에 포함이 된다.

3-Simplex는 어째서 Tetrahedron(사면체, 삼각뿔)이 되는지 설명하시오.
- a 0-simplex is a Point
- a 1-simplex is a Line Segment = aX + (1-a)Y 로 표현됨. 계수가 1개가 들어감.
- a 2-simplex is a Triangle = aX + bY + (1-a-b)Z 로 표현됨. 계수가 2개 들어감
- a 3-simplex is a Tetrahedron = 계수가 3개 들어감.
Simplex이 되는 가장 큰 조건은 서로 선형독립이여야 한다는 것이다.
기존 삼각형에서 점을 추가하면 3-simplex가 될 수 없다. 선형독립이 되기 위해서는 3차원으로 가야한다.
Cohen-Sutherland 알고리즘의 원리를 정리하시오.
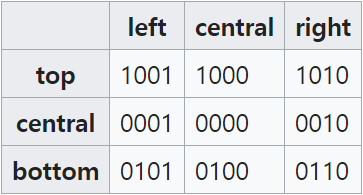
1. 두 지점을 확인하고 각 지역을 결정
2. 테스트 결과가 0 인 경우 선이 중앙 영역 0000 내부에 있음을 의미합니다.
3. 비트 테스트와 두 테스트의 작동 결과가 0이 아니면 라인이 중앙 영역 외부에 있음을 의미합니다. 그 줄을
건너 뛸 수 있습니다
4. 각 위치를 잘라서 가장자리 위치를 찾습니다.
Cohen-Sutherland 알고리즘을 구현한 코드와 움짤을 첨부하시오.
// Center = 0, Left = 1, Right = 2, Bot = 4, Top = 8
int WindowsRSI::TestRegion(const Vector2& InVectorPos, const Vector2& InMinPos, const Vector2& InMaxPos)
{
int result = Center;
if (InVectorPos.X < InMinPos.X) result = Left;
else if (InVectorPos.X > InMaxPos.X) result = Right;
if (InVectorPos.Y < InMinPos.Y) result = Bot;
else if (InVectorPos.Y > InMaxPos.Y) result = Top;
return result;
}
bool WindowsRSI::CohenSutherlandLineClip(Vector2& InOutStartPos, Vector2& InOutEndPos, const Vector2& InMinPos, const Vector2& InMaxPos)
{
float x0 = InOutStartPos.X;
float x1 = InOutEndPos.X;
float y0 = InOutStartPos.Y;
float y1 = InOutEndPos.Y;
int tr0 = TestRegion(InOutStartPos, InMinPos, InMaxPos);
int tr1 = TestRegion(InOutEndPos, InMinPos, InMaxPos);
bool accept = false;
while (true) {
if ((tr0 | tr1) == 0) {
accept = true;
break;
}
else if ((tr0 & tr1) > 0) {
//시작과 끝이 측면에 있음.
break;
}
else {
float x = 0;
float y = 0;
int trOut = tr0 > 0 ? tr0 : tr1;
float k = (y1 - y0) / (x1 - x0);
// y = y0 + k(x-x0)
// x = x0 + 1/k*(y-y0)
if ((trOut & Top) > 0) {
y = InMaxPos.Y;
x = x0 + (y - y0) / k;
}
else if ((trOut & Bot) > 0) {
y = InMinPos.Y;
x = x0 + (y - y0) / k;
}
else if ((trOut & Left) > 0) {
x = InMinPos.X;
y = y0 + (x - x0) * k;
}
else if ((trOut & Right) > 0) {
x = InMaxPos.X;
y = y0 + (x - x0) * k;
}
if (trOut == tr0) {
x0 = x;
y0 = y;
tr0 = TestRegion(Vector2(x, y), InMinPos, InMaxPos);
}
else
{
x1 = x;
y1 = y;
tr1 = TestRegion(Vector2(x, y), InMinPos, InMaxPos);
}
}
}
if (accept) {
InOutStartPos.X = x0;
InOutStartPos.Y = y0;
InOutEndPos.X = x1;
InOutEndPos.Y = y1;
}
return accept;
}
구현한 코드를 순서도로 정리하시오.

STL map이 사용하는 자료구조에 대해 조사하고 해당 자료구조는 어떤 특징이 있는지 자세하게 정리하시오.
- <key, value> 연관 컨테이너이다. // map<Key, Value> 변수이름
- 맵은 자동 정렬이 됨.
- 검색 속도가 일렬 방식(list, vector) 보다 빠름.
- Red-Black 트리 구조임(균형 이진 트리).
Red-Black Tree란?
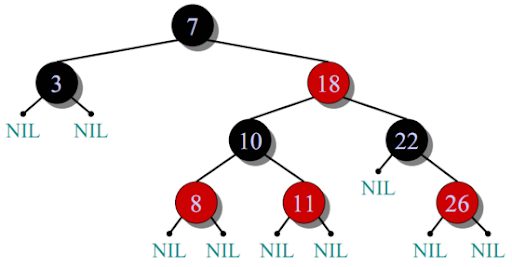
- 트리의 모든 노드는 검정색 아니면 빨간색이다.
- 루트 노드는 무조건 검정색이다.
- 모든 잎 노드는 검정색이다.
- 빨간색의 노드 자식들은 모두 검정색이지만, 검정색 노드 자식들은 어느 색깔이든 상관없다.
- 루트 노드에서 모든 잎 노드 사이에 있는 검정색 노드의 수는 모두 동일하다.
STL map이 가지는 단점은 무엇인지 정리하시오.
- 삽입 삭제가 빈번하면 안됨.(약간의 오버 헤드가 있음) // 할 때 마다 정리하기 때문에
- 해쉬맵이 아니다(O(1)) // Java는 기본적으로 hash_map임. O(1)
- 자동으로 정렬된다.
STL map 활용시 주의할 사항에 대해 정리하시오.
- nullPtr 검사 시 []연산자 대신 find() 함수를 사용해야 한다.
std::map<int, Character*> map
for(int i=0; i<100; ++1) {
Character* newChar = new Character();
map[i] = newChar
}
int checkIndex = 101;
if(map[checkIndex] == nullptr) // 잘못 된 접근이다. 이 순간 새 원소가 생성된다.
if(map.find(checkIndex) == map.end()) // 로 설정해야합니다.STL map과 unordered_map의 차이와 장단점에 대해 조사하시오.
차이점
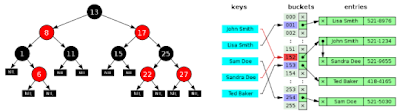
- STL map : Red-Black Tree를 사용해 키의 순서를 유지한다.
- unordered_map : 해시 테이블을 사용해 키의 순서를 유지하지 않는다.
- STL map: 시간 복잡도가 O(logN)이다
- unordered_map : 시간 복잡도가 O(1)이다.
장단점
- 데이터 크기 N 이 작을 땐 Map, 클 때는 unordered_map이 유리하다.
- map은 데이터 크기 N이 커짐에 따라 unordered_map 보다 캐시 미스의 영향을 더 빨리 받는다.
(map이 탐새개을 위해 여러 노드를 방문해야 하기 때문)
- unordered_map은 해시 함수의 성능이 중요하다.
- 문자열 키를 사용하는 경우 정수 키를 사용하는 경우에 비해 map이 더 큰 N까지 탐색 성능 우위를 가진다.
(문자열 비교에 적은 비교 횟수를 필요로 하기 때문)
- 문자열 길이가 길고 데이터 크기가 크지 않는 경우에는 map이 unordered_map 보다 탐색에 유리하다.
STL vector 활용에서 linear_search와 binary_search 의 차이와 장단점에 대해 조사하시오.
차이점
- linear_search : 시간 복잡도가 O(n) 이며, 정렬이 되지 않는다. 또한 순차적으로 수행한다.
- binary_search : 시간 복잡도가 O(logN)이다. 정렬이 된다. 또한 데이터를 임의로 수행한다.


시간 복잡도가 빠른 순 : O(logn) > O(n) > O(nlogn) > O(n^2) > O(n^3) > O(2^n) > O(n!)
시간들의 설명
- O(1) : 입력자료의 수에 관계없이 일정한 실행시간을 갖음
- O(logn) : 입력자료의 수에 따라 시간이 흐를수록 시간이 조금씩 증가
ex) 큰 문제를 일정한 크기를 갖는 작은 문제로 쪼갤 때 나타남
ex) 이진탐색 같은 효율이 좋은 검색 알고리즘
- O(n) : 입력 자료의 수에 따라 선형적인 실행 시간이 걸리는 경우 - 입력자료마다 일정 시간 할당
- O(nlogn) : 큰 문제를 일정 크기 갖는 문제로 쪼개고(logn+logn+ .. + logn) 다시 그것을 모으는 경우
ex) 효율 좋은 정렬 알고리즘
ex) quick sorting / heap sorting 등
- O(n^2) : 이중 루프내에서 입력 자료를 처리할 때
ex) 인접행렬이용한 bfs/dfs 알고리즘
- O(n^3) : 삼중 루프 내에서 입력자료 처리할 때
이미지 출처 : https://www.blog.dustinlee.me/221409956811
http://ddmix.blogspot.com/2015/02/cppalgo-19-red-black-tree.html
https://www.geeksforgeeks.org/linear-search-vs-binary-search/
'게임제작기법연구' 카테고리의 다른 글
| 게임제작기법연구 7주차 (0) | 2020.05.26 |
|---|---|
| 게임제작기법연구 6주차 (0) | 2020.05.19 |
| 게임제작기법연구 4주차 (0) | 2020.05.05 |
| 게임제작기법연구 2주차 (0) | 2020.04.09 |
| 게임제작기법연구 1주차 (0) | 2020.04.07 |